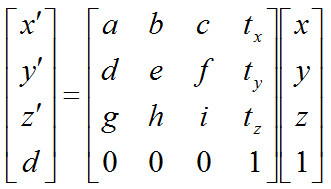|
Engineering Math - Matrix |
||
|
Affine Mapping/Affine Transformation
Affine Mapping is an area of applying Matrix to geomatric transformation. This is a linear transformation (the same transform is applied to every points of the object being transformed).
Let's take an intuive approach first.
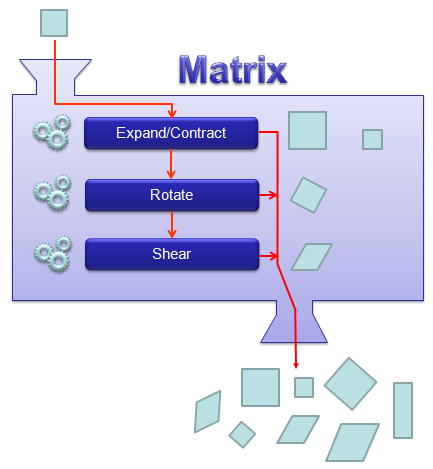
My own image for a matrix is a kind of machine that is doing things as follows. As you see in the illustration, Matrix is taking in a shape (geometrical shape/object) and transform (change shape) them in mainly three different way as follows. i) Scale (magnify or shrink) ii) Rotate iii) Shear(Skew) iv) Reflection In reality, a matrix can do more than one type of transformation like "Scale and Skew", "Scale and Rotate and Skew" etc. I will talk about this kind of transformation in this section and I hope you can have some intuitive understanding of the propery of a matrix since it can be visualized as in this section.
I think one of the best way to understand the characteristics of a Matrix is to apply it for an shape in a graphical coordinates and observe the result. Of course, there would be a certain limitation in this method since we can only visualize three dimensional shape and as a result the dimension of the matrix we can visualize would be 3 x 3 (or 4 x 4 in some cases). But if you build up a solid intuitive understanding of a properties of a matrix in this way, you can easily extend the understanding to any size of the matrix and, more importantly, you can understand more easily a mathematical model represented in the matrix format.
I will use a shape in two dimensional coordinate and 2 x 2 matrix applying to the shape on the coordinate. Here you see coordinates labeled (x1,y1) and (x2,y2). (x1,y1) represents each points before it is transformed by the matrix and (x2,y2) is the new points after (x1,y1) is transformed by the matrix.
Let's look at the first case. The first matrix is what we call Identity Matrix which has the value '1' in all the elements on diagonal line running from left top to right bottom and all the other elements are set to be '0'. What is the result of the transformation of a shape transformed by the Identity Matrix ? The answer is "No change".
Next look at another matrix shown below. This matrix also looks similar to diagonal matrix but not exactly same. The difference is that the first element on the diagonal line is '-1' in stead of '1'. What is the result ? The shape is flipped around y axis.
Next look at another matrix shown below. This matrix also looks similar to diagonal matrix but not exactly same. The difference is that the second element on the diagonal line is '-1' in stead of '1'. What is the result ? The shape is flipped around x axis.
Next look at another matrix shown below. In this case, all the elements on the diagonal lines is set to be '-1' instead of '0'. What is the result ? It became reflected around the point (0,0). You can interpret this in two steps. At the first step, the shape is flipped around y axis. and at the second step the shape is fliped around x axis.
Now let's look at another matrix as shown below. This time you see all '0's on the diagonal line and now you see a non-zero value out side of diagonal line. What is the result ? The image shears.
Now let's look at another matrix as shown below. This time you see the non-zero value in all the elements. This is tricky to analyze since these matrix can do almost everything described above.. but if the numbers in the elements can be represented as trigonometrix functions in the following format. This matrix can rotate the image as shown below.
Actually this is only a few of the examples.. you can try any numbers in the matrix and apply to some shape and try to correlate those numbers to the result of the transformation until you build up your own intuition of figuring out the characteristics of a matrix.
Now let's do a little bit of math. But don't get scared .. it is not complicated. In some country, you would have learned this level of mathematics in high school. In some country, you would learn this in very early chapters of linear algebra. So in terms of calculation, this is very simple. Just focus on understanding the meaning of the math.
Transformation without translation
The first case is the one where we apply transformation only and no translation, meaning transformation without any shifting. It means the object will change only its shape but does not change the position. (Transformation means 'changing the shape' and translation means 'changing the position'). In this case, the mathematical expression for this can be represented as follows. Try to understand the meaning of each terms.
In case of transformation in 2 D plane, the equation can be represented as follows. Depending on what value you put as a,b,c,d, you can perform any transformation (scaling, shearing, rotation, reflection).
In case of transformation in 3 D space, the equation can be represented as follows. Depending on what value you put as a,b,c,d,e,f,g,h,i, you can perform any transformation (scaling, shearing, rotation, reflection).
Now the question is 'which value I have to plug into this matrix to achieve the transformation that I want'. Following shows the matrix for some basic transformation.
If you plug in numbers as shown below in 2D transform matrix, the object stay same (does not change the shape)
If you plug in numbers as shown below in 3D transform matrix, the object stay same (does not change the shape)
If you plug in numbers as shown below in 2D transform matrix, you can magnify or shrink the shape. Depending on which value you put in Sx, Sy, the degree of scaling varies. Sx determines the scaling in x direction and Sy determines the scaling in y direction.
In 3D, the scaling matrix is defined as follows :
Note : If you want to see this transformation in more intuitive way, check these pages : scaling along X axis, scaling along Y axis, scaling along Z axis in www.slide4math.com
If you plug in numbers as shown below in 2D transform matrix, you can shear the object. The value of Sh determines the degree of shear.
If you plug in numbers as shown below in 3D transform matrix, you can shear the object. The value of Sh determines the degree of shear. You can move Sh to different location to do shearing in different direction.
Note : If you want to see this transformation in more intuitive way, check these pages : S12, S13, S21, S23, S31, S32 in www.slide4math.com
If you plug in numbers as shown below in 2D transform matrix, you can rotate the object around the center of the coordinate (0,0) .
Note : If you want to see this transformation in more intuitive way, check this page in www.slide4math.com
In 3D case, rotation gets a little complicated. We need to think of the rotation around each axis separately as shown below.
Note : If you want to see this transformation in more intuitive way, check these pages : rotation around X axis, rotation around Y axis, rotation around Z axis in www.slide4math.com
Transformation with translation
Now let's think of the case where both transformation (chaning shape) and translation (changing the position) is applied. The mathemtication expression of this change is represented as follows.
If you expend this equation into real matrix and vector, you will have the following form for 2D.
and you will have the following form in 3D.
The mathematical equation itself is simple.
Now you may have a question : Is there any way to combine the transformation component and translation component into a single matrix ?
The first guess you may have would be just to combine the two components as follows. But this is impossible because it is impossible to do calculation in this form.
The most common solution for this case is to add another row as follows.
Then you might ask how do you know if this is proper combining. How do you prove this matrix would successfully combine the transformation process and translation process ? It is simple. Just do to calculate the matrix equation and see it the resulting equation matches the transformation+translation equation I showed you at the beginiing. See the check-up process shown below.
In the same logic as explained, you can create a matrix to perform 'transformation + translation' in 3D as shown below.
|
||