|
Physics Modeling
Using neural networks and machine learning (ML) for studying physics marks a big change towards using data to understand complicated physics problems. This method uses artificial intelligence to study, predict, and create simulations of physics events. It often does better than older methods in being correct and fast.
Putting neural networks and ML into physics study is a good step that adds to the older ways of analyzing and calculating physics. By using data-based methods, scientists can solve difficult physics problems with great accuracy and speed. But, the success of these methods relies on solving issues with understanding how they work, needing lots of good data, and making sure the methods work well on new problems. As this area grows, the teamwork between ML and physics is expected
to get stronger. This will lead to new findings and better understanding of the physics world
Applications in Physics
Followings are a list of common applications :
Advantages and Challenges
Neural networks offer powerful tools for physics modeling, capable of handling complex systems with high efficiency and adaptability. However, their success depends on the availability of high-quality data, computational resources, and the ability to interpret and generalize their findings. Balancing these pros and cons is essential for effectively leveraging neural networks in physics research.
-
Pros
- Cons
- Black Box Nature: It's often hard to understand how neural networks make their predictions, which can be a problem for scientific fields that value transparency and understanding the underlying principles.
- Data Dependency: Their performance heavily relies on the quantity and quality of the data. Poor or biased data can lead to inaccurate models.
- Overfitting: Neural networks can become too tailored to the training data, making them perform poorly on new, unseen data.
- Resource Intensive: Training neural networks, especially deep learning models, requires significant computational resources and energy, which can be a barrier for some projects.
- Generalization Issues: While neural networks are adaptable, they may struggle to generalize their findings to situations that are not represented in the training data.
Models and Examples
There are many kinds of different model we can use for physics modeling and which model to use depends on applications.
Fully Connected Feedforward Networks (Multilayer Perceptrons, MLPs)
Introduction: Fully connected feedforward networks, also known as Multilayer Perceptrons (MLPs), are among the simplest types of neural networks. They consist of one or more hidden layers of neurons where each neuron in one layer is connected to every neuron in the next layer. MLPs are versatile and can be used for a wide range of physics modeling tasks, especially when dealing with well-defined problems that do not inherently involve spatial or temporal data. Their straightforward structure
makes them an excellent starting point for many applications.
- Examples: MLPs are used for regression tasks, classification problems, and even for solving differential equations in physics. They can model relationships between inputs and outputs where the spatial or temporal arrangement of data is not the primary concern.
- Input: Numerical data vectors that represent physical quantities (e.g., temperatures, pressures, material properties).
- Output: Predictions of physical quantities, classifications (e.g., phase identification), or solutions to equations.
- Pros:
- Simplicity: MLPs have a straightforward architecture, making them easier to understand and implement compared to more complex models like CNNs or RNNs.
- Versatility: They can handle a wide range of tasks, from simple regressions to complex nonlinear mappings.
- Ease of Training: With fewer hyperparameters than more complex networks, MLPs can be easier to train, requiring less computational resources.
- Cons:
- Limited Context Understanding: Without the mechanisms to process sequential or spatial data, MLPs might not perform as well as CNNs or RNNs on tasks that heavily rely on the spatial arrangement or temporal sequence of data.
- Overfitting: They can easily overfit to the training data, especially when the network is too large or the data is limited, leading to poor generalization to unseen data.
- Handling Complexity: While versatile, MLPs might struggle with very complex problems that involve intricate relationships or high-dimensional data, where models like CNNs or RNNs might be more suitable.
Convolutional Neural Networks (CNNs)
Introduction: Convolutional Neural Networks (CNNs) are specialized for processing data with a grid-like topology, such as images. CNNs use convolutional layers to automatically and adaptively learn spatial hierarchies of features from input images or spatial data. This makes them exceptionally good for applications in physics that involve spatial data analysis, such as phase detection from microscopic images or pattern recognition in particle physics experiments.
- Examples: Used in image-based analysis in physics, such as identifying phases of matter or analyzing particle tracks in high-energy physics experiments.
- Input: Images from experiments or simulations (e.g., patterns formed in particle collisions).
- Output: Classification of images into categories (e.g., identifying different phases of materials) or extraction of features (e.g., energy levels, particle types).
- Pros:
- Efficient Image Processing: CNNs excel at handling grid-like data (such as images), making them highly efficient for image-based analysis.
- Feature Extraction: Automatically detect important features without manual intervention.
- Cons:
- Interpretability: It's challenging to understand how CNNs identify and use specific features from images.
- Data Requirement: Effective training requires large sets of labeled images.
Recurrent Neural Networks (RNNs)
Introduction: Recurrent Neural Networks (RNNs) are designed to handle sequential data, making them ideal for modeling time-dependent physics phenomena. Unlike feedforward networks, RNNs have loops allowing information to persist, mimicking a form of memory. This capability makes RNNs suitable for analyzing time series data or predicting the evolution of physical systems over time.
- Examples: Modeling time-dependent phenomena in physics, like predicting the evolution of a physical system over time.
- Input: Sequential data or time series data (e.g., temperature changes, particle motion).
- Output: Future states of the system or time series forecasting.
- Pros:
- Temporal Dynamics Handling: RNNs are designed to handle sequences, making them suitable for time-dependent physical processes.
- Memory Capability: Can remember information from previous inputs for making predictions.
- Cons:
- Gradient Vanishing/Exploding: Training difficulties due to the gradients either vanishing or exploding in long sequences.
- Complexity: More complex to train and tune compared to some other network types.
Generative Adversarial Networks (GANs)
Introduction: Generative Adversarial Networks (GANs) consist of two networks, a generator and a discriminator, that are trained simultaneously through a form of contest. The generator tries to produce data that is indistinguishable from real data, while the discriminator attempts to distinguish between real and generated data. GANs are particularly useful in physics for generating synthetic data that can be used for training other models or for augmenting datasets where collecting real experimental
data is costly or difficult.
- Examples: Generating new data instances that resemble the training data, such as simulating particle physics events or generating synthetic datasets for training other models.
- Input: Random noise (for the generator); real data instances and generated data instances (for the discriminator).
- Output: Synthetic data instances that are indistinguishable from real data.
- Pros:
- Data Generation: Can generate new data instances for further analysis or training.
- Innovative Applications: Useful for data augmentation and simulating conditions not seen in experiments.
- Cons:
- Training Stability: GANs are notoriously difficult to train; achieving equilibrium between the generator and discriminator can be challenging.
- Quality of Output: The quality of generated data can vary, requiring careful evaluation.
Deep Reinforcement Learning (DRL)
Introduction: Deep Reinforcement Learning combines reinforcement learning with deep neural networks to enable models to make decisions and learn policies based on rewards. DRL is used in physics for optimizing experimental setups or controlling physical processes dynamically. It's particularly effective in scenarios where a model needs to learn how to achieve a goal in a complex environment, adjusting its actions based on feedback from the environment.
- Examples: Optimizing experimental setups in physics or controlling physical processes (e.g., tuning the parameters of a particle accelerator).
- Input: State of the environment (e.g., current setup parameters, physical measurements).
- Output: Actions to achieve a certain goal (e.g., adjustments to the experimental setup).
- Pros:
- Decision Making: Capable of learning complex decision-making strategies to optimize outcomes.
- Adaptability: Can continually learn and adapt to changing environments.
- Cons:
- Sample Efficiency: Requires a lot of interactions with the environment for learning, which can be impractical in many physical settings.
- Complexity and Cost: Developing and training DRL models can be resource-intensive and costly.
Encoder-Decoder model
An Encoder-Decoder model, often associated with sequence-to-sequence (seq2seq) learning, is a powerful neural network architecture used to map sequences to sequences. This type of model is particularly useful in physics for problems where the input and output are sequences that can represent time series data, spatial distributions, or transformations from one state to another. A compelling application of Encoder-Decoder models in physics is in the field of particle physics event classification
or forecasting physical processes over time.
- Example: Forecasting Solar Activity
- Objective: Predict future solar activity, such as sunspot numbers or solar flare occurrences, based on past activity records. This task is crucial for understanding space weather and its potential impact on Earth's communication systems.
- Input: Time series data of solar activity measurements, such as daily sunspot numbers, solar flux, or magnetic field measurements over a period.
- Output: A forecasted sequence of solar activity measurements for a future time period.
- Process:
- Data Preparation: The historical solar activity data is divided into sequences that serve as the input and output for training. For example, using the past 60 days of sunspot numbers to predict the next 7 days.
- Model Training:
- The encoder processes the input sequence and compresses the information into a context vector, capturing the essential features of the past solar activity.
- The decoder takes this context vector and generates the output sequence, predicting future solar activity.
- Model Evaluation: The model's predictive accuracy is assessed using a separate test set, comparing the predicted solar activity against actual observations.
- Pros:
- Temporal Relationship Learning: The Encoder-Decoder architecture is adept at capturing temporal dependencies, making it ideal for forecasting tasks where past events influence future outcomes.
- Flexibility: This model can handle variable-length input and output sequences, accommodating fluctuations in data availability and the desired forecasting horizon.
- Cons:
- Complexity: Encoder-Decoder models can be complex and require substantial data for training to effectively capture the dynamics of the physical process.
- Data Dependency: The quality of the forecast relies heavily on the quantity and quality of the historical data. Inaccurate or incomplete data can significantly impair the model's performance.
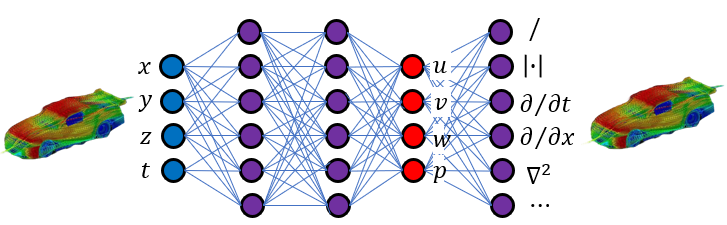
- Example: Solving Differential Equations Using Encoder-Decoder Models
- Objective: To solve complex differential equations that describe a physical system, which can be challenging with traditional numerical methods due to high nonlinearity or computational cost.
- Input: The inputs to the model are the parameters and initial conditions of the differential equation. This might include spatial coordinates, time points, and initial state values of the system.
- Output: The output is the solution to the differential equation over time or space, such as the evolution of a physical state or the distribution of a quantity.
- Process:
- Data Preparation: Generate or collect data representing solutions to the differential equations under various conditions. This could involve running simulations with known physics-based models to create a dataset of input conditions and corresponding outputs.
- Model Architecture: The encoder part of the model learns to understand and compress the input conditions into a dense representation, capturing the essential information needed to solve the equation. The decoder then uses this representation to generate the solution to the differential equation, step by step if necessary, across the desired range of conditions.
- Training: Train the model on the dataset, using a loss function that accurately measures the difference between the predicted solutions and the actual solutions from the dataset.
- Evaluation and Testing: Validate the model's ability to solve the differential equations accurately on a set of test cases not seen during training, ensuring its generalizability and accuracy.
- Pros:
- Handling Complexity: Encoder-Decoder models can manage the complexity of solving differential equations that are difficult for traditional methods, especially in high-dimensional spaces or when the equations are highly nonlinear.
- Efficiency: Once trained, these models can solve equations much faster than numerical simulation methods, offering significant computational savings.
- Cons:
- Data Dependency: The model's performance is heavily dependent on the quality and diversity of the training data. Generating this data can be computationally expensive.
- Interpretability: Similar to other neural network models, the "black box" nature makes it difficult to understand how the model is solving the equations, potentially limiting insights into the physical system's behavior.
YouTube
Reference
|
|
