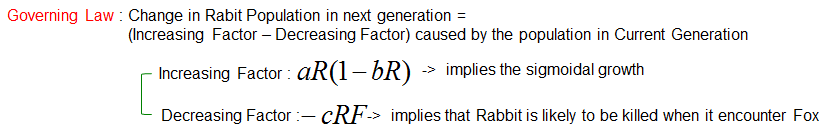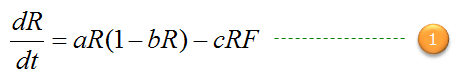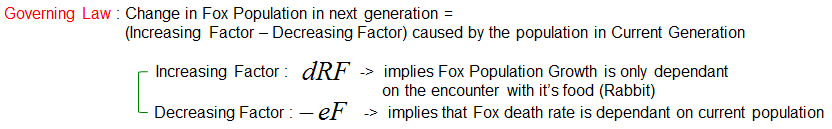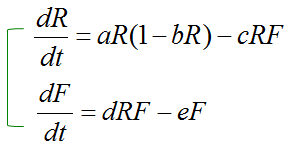The prey and predator model offers a fascinating lens to understand the intricate balance of ecosystems, where survival is a constant interplay of growth and decline. At its core, this model reflects how populations of two species—such as rabbits and foxes—are not just interdependent but dynamically influence each other over time. While intuition might suggest simple cause-and-effect relationships, like more predators leading to fewer prey, the reality is far more nuanced. The feedback loop inherent in this interaction—where predator populations depend on prey abundance, and prey populations are controlled by predation—creates oscillations rather than straightforward outcomes.

For instance, a temporary abundance of rabbits might fuel a rise in fox populations, but as prey becomes scarce, predators face resource shortages, triggering their decline. This cyclical pattern is a hallmark of predator-prey dynamics, rooted not just in hunting behaviors but also in environmental factors, reproductive rates, and even chance events. Mathematical models like the Lotka-Volterra equations help untangle these complexities by providing tools to predict when populations stabilize, peak, or crash. These models reveal that what seems chaotic at first glance is governed by underlying principles—principles that can illuminate broader ecological and even societal systems where resources and consumers are in flux.

Let's approach with intuition

Let's start with an Intuitive approach. Let's assume that you are oberving a Rabit population and Fox population in an area. And by common sense and observation, you would know Fox hunts Rabits meaning Fox is the predator and Rabit is the prey in the area.

Without using any math and just using your intuition, think of what would happen if the number of Fox would increase in the area ?

You may easily think that the number of Rabit will decrease because more and more rabbits will be killed by Fox.

It is easy.

Then, will all the rabit will be eaten by Fox and they will completely disappear ?

The answer to this question is not easy. The answer can be 'Maybe Yes, Maybe No. The answer would depend on the population changes of Fox and how fast the fox eats away rabits etc.

To get the answer to this kind of tricky question you need to use mathematical modeling and understand the exact relationship between the two populations.

Again only using your intuition, think of what will happen when the birth rate of Rabit increases and the number of Rabit increases ?

You may easily guess that the number of Fox will increase as well because they get food more easily.

Then, will this situation goes forever ? Will fox hunt rabit such easily forever ?

Probably not, because as fox hunt rabit more easily and the number of fox increases, at some point the number of rabit may decrease since too many rabits are hunted.

Decreasing number of rabbit means decreasing food for Fox and eventually the number of Fox will decrease as well.

Now you may roughly understand the inter-relationship between Rabbit population and Fox population. But if I ask you about exactly when the rabbit popuation would grow or shrink or exactly when the fox popuation would grow or shrink. You cannot answer this questions without exact mathematical modeling of those population changes.

In this note, we will derive very basic models of these population changes using differential equation.

How Rabbit Population Changes ?

First let's think of the rule (Governing Law) for the population change of the rabit. It can be described as follows.

Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the rabbit as follows.

This equation represents the delicate balance of growth and decline in a rabbit population, governed by natural reproduction, environmental constraints, and predation by foxes. The first term, aR(1 - bR), models how the rabbit population grows in ideal conditions but slows as the population approaches its carrying capacity, reflecting the limits imposed by finite resources. The second term, -cRF, introduces the predator's role, showing how the interaction between foxes and rabbits directly impacts the rabbit population through predation. Together, these terms encapsulate the dynamic tension between self-regulated growth and external pressures, offering a window into the oscillatory nature of predator-prey systems. This interplay is not static; it reflects a dynamic feedback loop where each population's changes ripple through the ecosystem, demonstrating how complex, interdependent forces shape the survival of species over time. Understanding these dynamics mathematically reveals patterns that intuition alone often overlooks, helping to predict the ebb and flow of populations in nature.

The change in the rabbit population (dR/dt) over time is expressed as the difference between two terms:

Increasing Factor (aR(1 - bR))

• This represents the natural growth of the rabbit population in the absence of predators.
• a: The intrinsic growth rate of the rabbit population.
• 1 - bR: A limiting factor due to resource constraints or carrying capacity, where b is a constant indicating how quickly resources become limiting as the population grows.
• This term introduces sigmoidal growth, meaning the rabbit population grows rapidly when small but slows as it approaches the carrying capacity.

Decreasing Factor (-cRF)

• This represents the rate at which the rabbit population decreases due to predation by foxes.
• c: The rate at which rabbits are hunted by foxes (predation efficiency).
• RF: The interaction term between rabbit (R) and fox (F) populations, which reflects that the number of rabbits killed depends on both populations. More foxes and more rabbits increase the likelihood of predation.

Combining the Factors  :By combining these two factors, the model accounts for:

• Growth of rabbits driven by reproduction but limited by resources (aR(1 - bR)).
• Reduction in rabbit numbers due to predation (-cRF).

Insights from the Model

• Sigmoidal Growth: When foxes are absent or their population is negligible (F ≈ 0), the rabbit population grows sigmoidal due to the aR(1 - bR) term. Initially, it grows exponentially, but as the population approaches the carrying capacity, the growth slows and stabilizes.
• Predator-Prey Dynamics: When foxes are present (F > 0), the predation term (-cRF) counteracts growth. If the number of foxes is high, the rabbit population may decline significantly, even to extinction, depending on the balance between growth (aR) and predation (cRF).
• Balance and Oscillations: The interplay between growth and predation can lead to dynamic oscillations where rabbit and fox populations fluctuate over time, a hallmark of predator-prey systems.
• Dependency on Parameters: The values of a, b, and c determine the behavior of the system. For instance, a higher predation efficiency (c) or a smaller carrying capacity (b) can lead to drastic changes in population dynamics.

How Fox Population Changes ?

Now let's think of the rule (Governing Law) for the population change of the fox. It can be described as follows.

Now just combine the increasing factor and decreasing factor and you can get a differential equation for the population changes of the fox as follows.

The rate of change of the fox population (dF/dt) is determined by:

Increasing Factor (dRF):This term reflects how the fox population grows due to successful predation on rabbits.

• d: The efficiency or rate at which foxes convert encounters with rabbits into population growth. Higher values of d indicate that predation more effectively contributes to reproduction or survival.
• RF: The interaction between rabbit and fox populations. A higher rabbit population (R) means more available food, leading to increased fox reproduction or survival. If rabbits are scarce, this term diminishes, slowing fox population growth.

Decreasing Factor (-eF): This term accounts for the natural decline of the fox population due to mortality, independent of rabbit availability.

• e: The mortality rate of foxes. A higher value of e means foxes are dying off more quickly.
• F: The current fox population. As the number of foxes increases, the absolute impact of mortality also increases proportionally.

Combined Equation  : The combination of these two factors gives the differential equation:

dF/dt = dRF - eF

This equation demonstrates that the fox population dynamics are primarily influenced by two elements: the availability of prey (which fuels growth) and the natural death rate (which causes decline). When prey is abundant, the first term (dRF) dominates, leading to fox population growth. Conversely, when prey is scarce, the second term (-eF) dominates, causing the fox population to shrink.

Insights from the model

• Dependence on Rabbits: The fox population is entirely dependent on the availability of rabbits for growth. Without rabbits (R = 0), the increasing factor (dRF) becomes zero, and the fox population can only decrease due to natural mortality. This emphasizes the predator-prey interdependence.
• Mortality’s Role: The mortality term (-eF) acts as a stabilizing factor. Even when prey is abundant, a high mortality rate (e) can limit fox population growth. This prevents unchecked predator expansion, which could lead to overhunting and collapse of the prey population.
• Dynamic Interplay: Over time, the interaction between these two terms creates oscillations. As rabbits increase, foxes grow, but this growth eventually leads to over-predation, reducing the rabbit population. With fewer rabbits, foxes face food shortages, leading to a decline in their numbers, which then allows the rabbit population to recover. This cyclical pattern is characteristic of predator-prey systems.
• Critical Balance: The values of d and e determine the stability of the ecosystem. If predation efficiency (d) is too high or fox mortality (e) is too low, the system can destabilize, leading to over-predation and possible extinction of both populations.

Putting Them Together

Now you have a two equations for rabbit and fox population. However, you cannot solve the two equation separately because Rabbit population equation has fox population as a part of the equation and Fox population equation has rabbit population as a part of the equation.

To get the solution for the two equation, you have to combine the two into a system equation (simultaneous equation) as show below and solve the system equation. For now, don't worry about solving the proplem. If you just understand the meaning of this equation, my goal is done. I will give you a graphical solution for this equation later.

By combining the two equations, this model captures the interwoven relationship between predators and prey. It provides a framework for understanding how ecological systems balance growth, decline, and interdependence. This foundation can be expanded to include additional complexities, such as external factors (e.g., seasonal changes, environmental disruptions) or multi-species interactions, making it a versatile tool in ecological modeling and conservation efforts.

The System of Equations

Rabbit Population Equation:

dR/dt = aR(1 - bR) - cRF

This equation describes the rate of change in the rabbit population (R) over time. The first term, aR(1 - bR), represents natural growth constrained by environmental limits (carrying capacity). The second term, -cRF, captures the loss of rabbits due to predation by foxes.

Fox Population Equation:

dF/dt = dRF - eF

This equation models the fox population (F). The first term, dRF, represents growth fueled by predation success, dependent on the availability of rabbits (R). The second term, -eF, reflects natural mortality within the fox population.

Interdependence of the Equations

These two equations are deeply interconnected: - The rabbit population equation (dR/dt) depends on the fox population (F) because predation affects the number of rabbits. - Similarly, the fox population equation (dF/dt) depends on the rabbit population (R) because the availability of prey determines the foxes' food supply and reproduction.

Thus, the behavior of one population cannot be isolated from the other. To predict how both populations will evolve over time, the equations must be solved together as a system.

Solving the System

To find a solution, the equations must be solved simultaneously. This involves:

Numerical Methods: Since analytical solutions are often impractical, numerical approaches (like Runge-Kutta methods) are typically used to approximate the populations over time.

Graphical Representation: The solutions are often visualized as time-series plots or phase portraits. A phase portrait illustrates the trajectories of the populations in the R-F plane, showing how they influence each other dynamically.

Dynamic Behavior and Insights

The dynamic behavior of the predator-prey system is characterized by a fascinating interplay of growth and decline that results in cyclical population patterns. This oscillatory behavior emerges naturally from the interactions between the rabbit and fox populations: an abundance of rabbits provides more food for foxes, causing their numbers to rise. However, as the fox population grows, predation intensifies, leading to a decline in the rabbit population. With fewer rabbits available, the fox population eventually decreases due to food scarcity, allowing the rabbit population to recover and restart the cycle. Beyond these oscillations, the system can also reach equilibrium points where both populations stabilize, though the stability of these points depends heavily on the initial conditions and parameters, such as predation efficiency and mortality rates. Small changes in these parameters can have profound effects, potentially destabilizing the system and leading to outcomes like population collapse or unchecked growth. This sensitivity to parameters highlights the delicate balance that governs the predator-prey relationship.

• Oscillatory Dynamics: The system often exhibits oscillatory behavior, where the rabbit and fox populations rise and fall cyclically. This reflects natural predator-prey interactions, such as: - An increase in rabbits leading to a rise in foxes (due to more food). - An increase in foxes causing a decline in rabbits (due to over-predation). - A decline in rabbits resulting in fewer foxes (due to food shortages). - Fewer foxes allowing the rabbit population to recover, restarting the cycle.
• Equilibrium Points: The system has equilibrium points where both populations stabilize. However, the stability of these points depends on the parameters (a, b, c, d, e) and the initial population sizes.
• Parameter Sensitivity: Changes in parameters like predation efficiency (c) or fox mortality (e) can drastically alter the system's dynamics, potentially leading to population collapse or runaway growth.